++ 50 ++ 30 60 90 triangle formula chart 769744-30 60 90 triangle formula chart

Special Triangles Isosceles and Calculator This calculator performs either of 2 items 1) If you are given a right triangle, the calculator will determine the missing 2 sides Enter the side that is known After this, press Solve Triangle 2) In addition, the calculator will allow you to same as Step 1 with a right triangleTriangles Theorem 2 In a triangle whose angles measure 30 0, 60 0, and 90 , the hypotenuse has a length 0 equal to twice the length of the shorter leg, and the length of the longer leg is the product of 3 And the length of the shorter leg The ratio of the sides of a triangle are x x 3 2 x Note The short leg is alwaysAlthough all right triangles have special features – trigonometric functions and the Pythagorean theoremThe most frequently studied right triangles, the special right triangles, are the 30, 60, 90 Triangles followed by the 45, 45, 90 triangles

Trigonometry For Dummies Cheat Sheet Dummies

30 60 90 triangle formula chart

30 60 90 triangle formula chart-We know that in a 3060=90 triangle, the smallest side corresponds to the side opposite the 30 degree angle Additionally, we know that the hypotenuse is 2 times the value of the smallest side, so in this case, that is 10 The formula for , so orA right triangle has a leg with a length of 18 and a hypotenuse with a length of 36 Bernie notices that the hypotenuse is twice the length of the given leg, and decides it is a triangle (a) How does Bernie know this a triangle?

A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation

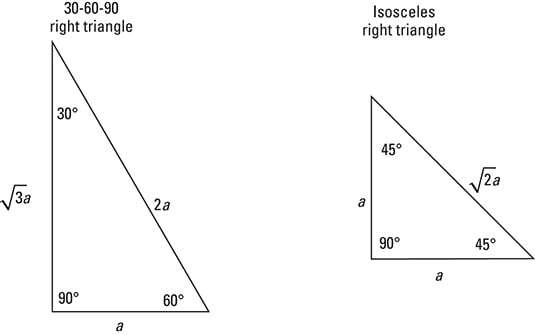
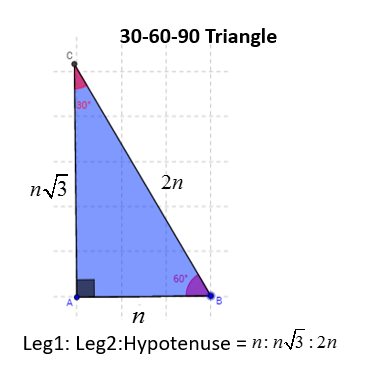
 The sides of a right triangle lie in the ratio 1√32 The side lengths and angle measurements of a right triangle Credit Public Domain We can see why these relations should hold by plugging in the above values into the Pythagorean theorem a2 b2 = c2 a2 ( a √3) 2 = (2 a) 2 a2 3 a2 = 4 a2A triangle is a particular right triangle because it has length values consistent and in primary ratio In any triangle, the shortest leg is still across the 30degree angle, the longer leg is the length of the short leg multiplied to the square root of 3, and the hypotenuse's size is always double the length of the shorter leg Here is a triangle with one side length given Let's find the length of the other two sides, x and y You are given the length of the hypotenuse in

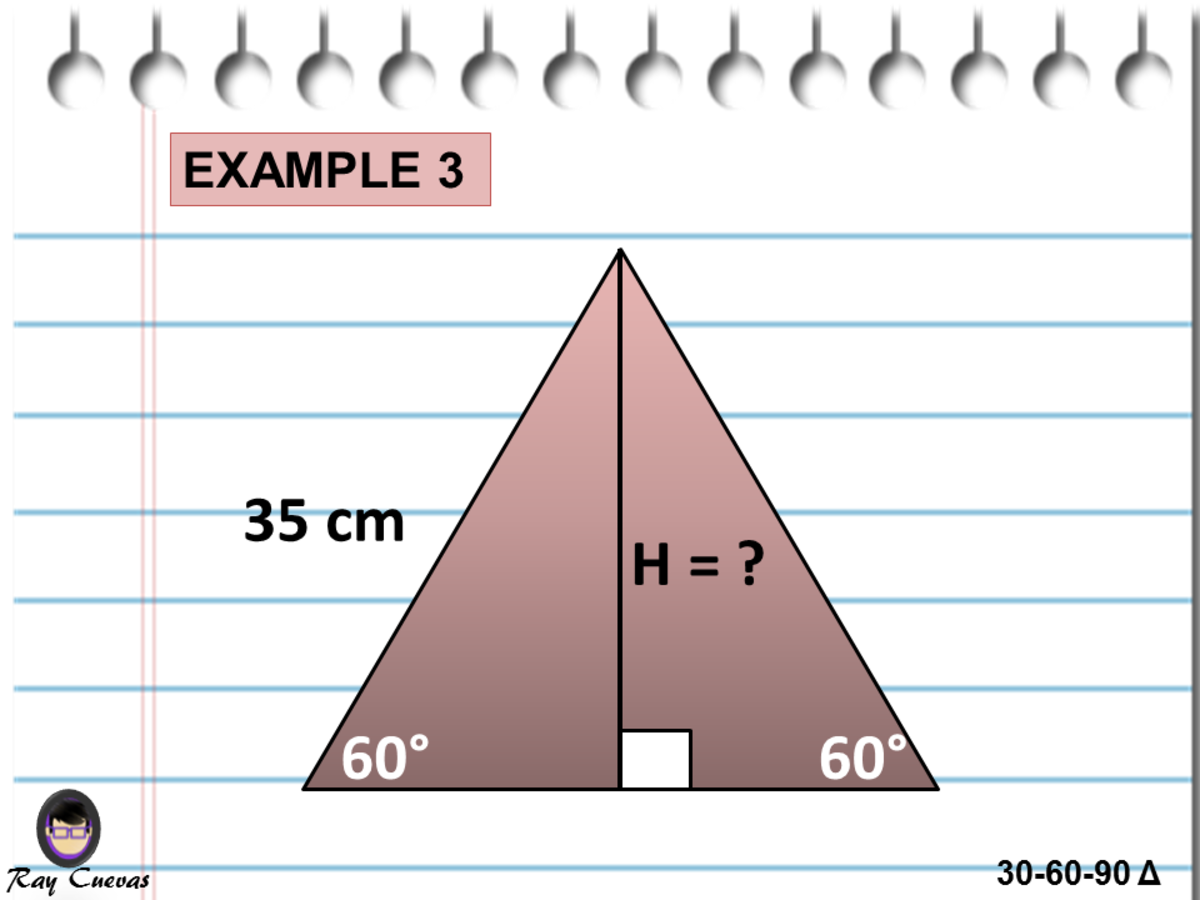
 When we are done with the right Triangle and various other unique right Triangles, it is time to experience the How To Work With degree Triangles 0The following special angles chart show how to derive the trig ratios of 30°, 45° and 60° from the and special triangles Scroll down the page if you need more examples and explanations on how to derive and use the trig ratios of special angles Thanks to this 30 60 90 triangle calculator you find out that shorter leg is 635 in because a = b√3/3 = 11in * √3/3 ~ 635 in hypotenuse is equal to 127 in because c = 2b√3/3 = 2a ~ 127 in area is 349 in² it's the result of multiplying

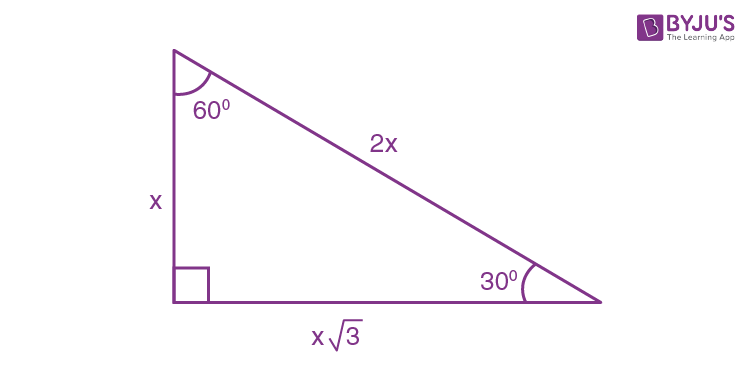
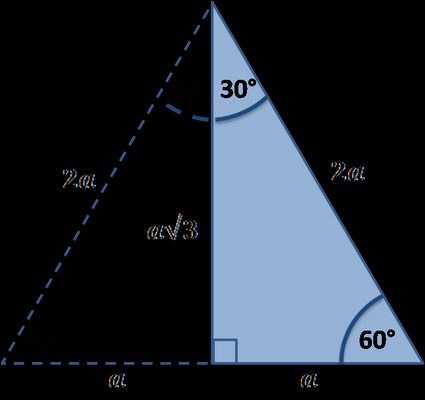
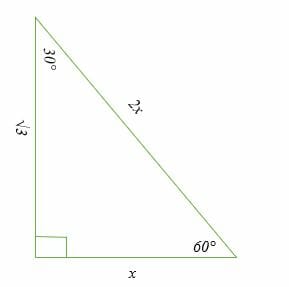
 60° x = 223, y = 22 12) u293 v 30° u = 58, v = 29 13) a36 b 60° a = 243, b = 123 14) x y 43 30° x = , y = 12 15) xy 45 60° x = 90, y = 453 16) x 323 y 30° x = 64, y = 32 17) 40 x y 30° x = 3, y = 18) x 333 2 y 30° x = 33, y = 33 2(b) Since this is a triangle, what should the remaining leg length be?The formulas for finding the rest of the triangle from just x are the following, where y = the long side, z = the hypotenuse, a = area, and p = perimeter • y = x*sqrt (3) • z = x*2 • a = x^2*sqrt (3/2) • p = x* (3 sqrt (3)) you might note that the triangle is exactly one half of an equilateral triangle a triangle with equal sides

The Complete Guide To The 30 60 90 Triangle Collegevine Blog

Special Right Triangles Ck 12 Foundation

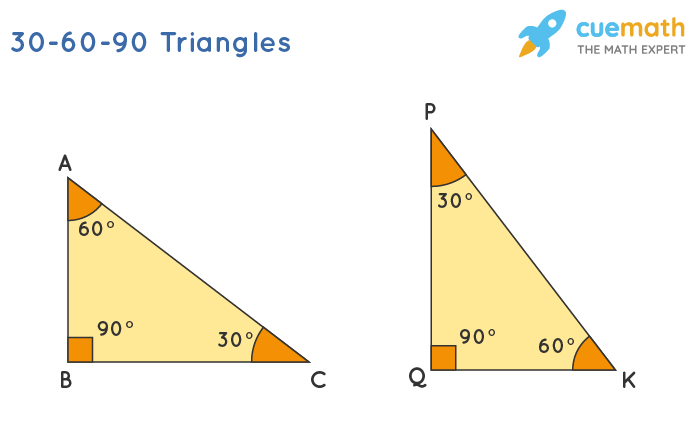
 Special Right Triangles long 30 hypotenuse leg 600 short leg 450 hypotenuse leg 450 leg short leg = hypotenuse long leg (short leg) hypotenuse = 2 (short leg) legs are equal hypotenuse = (leg) Use the and triangleAcross from the 60 degree angle is the secondbiggest side (in this caseA triangle is a right triangle whose internal angles are 30, 60 and 90 degrees The three sides of a triangle have the following characteristics All three sides have different lengths The shorter leg, b, is half the length of the hypotenuse, c That is, b=c/2 The longer leg's length, a, is the shorter leg times 3Thatis, a=b

2

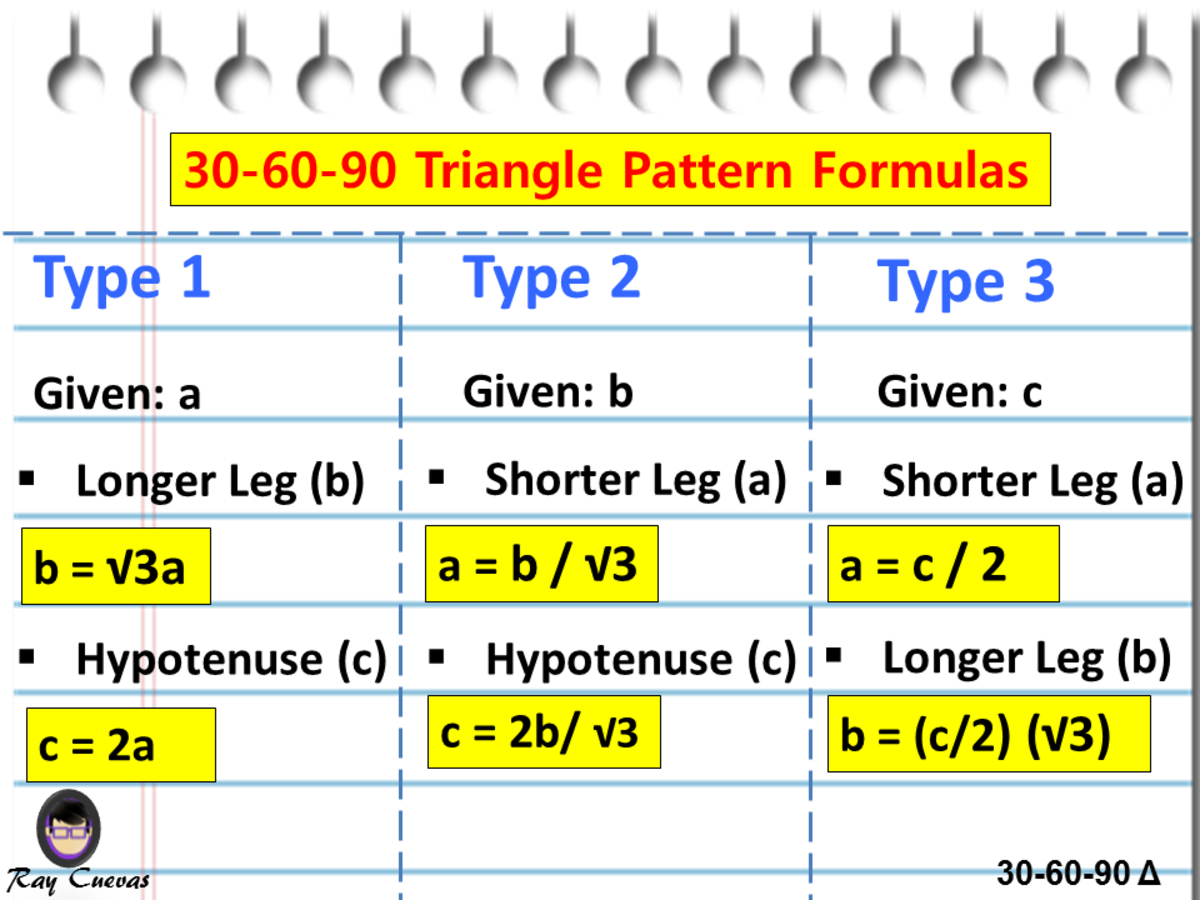
A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation

Distance formula dx=−()xy−()y 21 2 21 2 Slope of a line m yy xx = − − 21 21 Slopeintercept form of a linear equation ym=xb Pointslope form of a linear equation yy−=mx−x 11 Standard form of a linear equation AxBy=C STAAR GEOMETRY REFERENCE MATERIALS 30 ° 2 x x 60 ° x 3 30° – 60° – 90° triangle x x 45 ° 4542 printable unit circle charts diagrams sin cos tan, unit circle wyzant resources, special right triangles formulas 30 60 90 and 45 45 90, unit circle w everything charts worksheets 35 examples, special right triangles chart theresetA right triangle (literally pronounced "thirty sixty ninety") is a special type of right triangle where the three angles measure 30 degrees, 60 degrees, and 90 degrees The triangle is significant because the sides exist in an easytoremember ratio 1 √3 3 2 That is to say, the hypotenuse is twice as long as the shorter leg, and

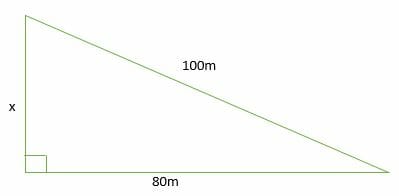
3 4 5 Right Triangles Explanation Examples

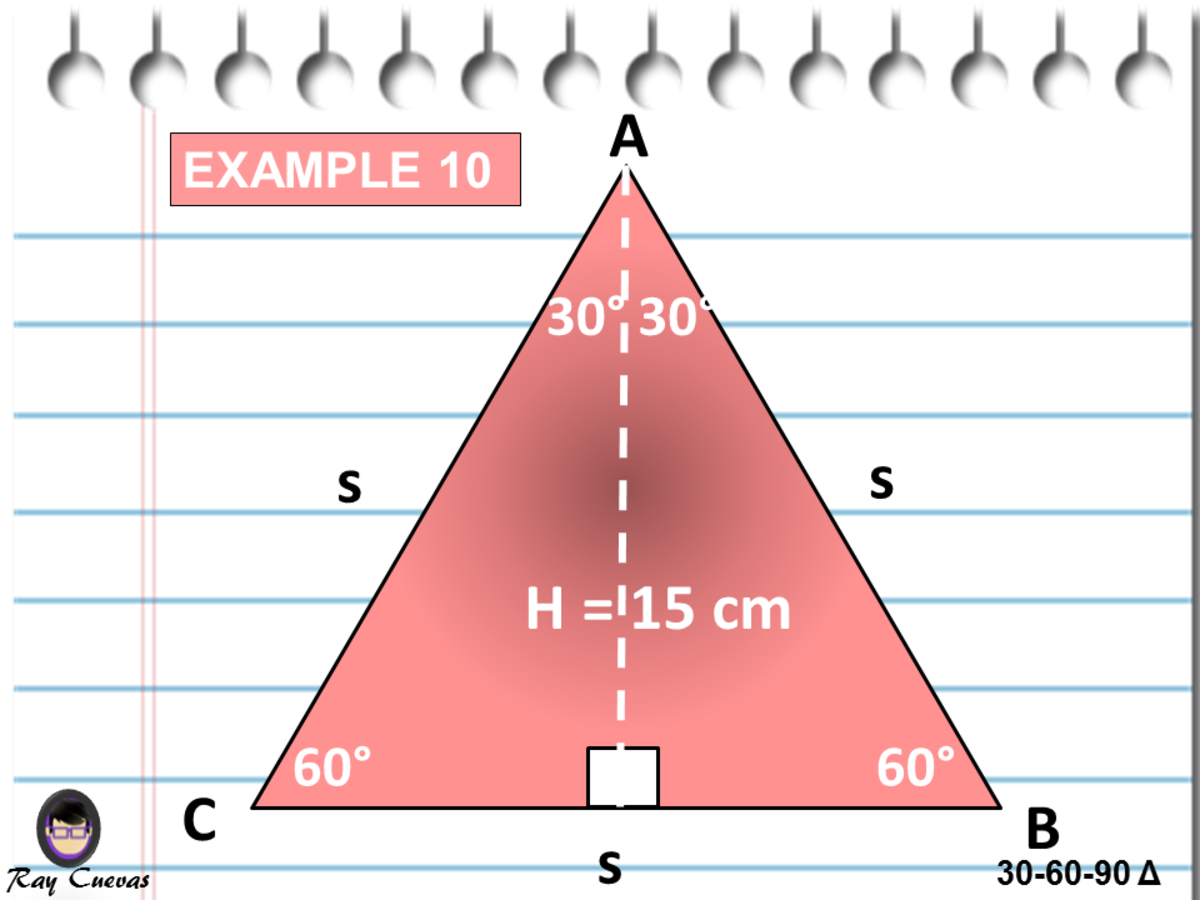
A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation

 All you have to do is recall the triangles formula which was shared ealier which is x2xx\sqrt3 and apply it From our formula, we can find the value of our two other sides just by inputing the given value into the equation Where x is equals 5, the hypotenuse (2x) becomes 2 \times 5 = 10, while the adjacent side becomes x\sqrt {3 We can use the Pythagorean theorem to show that the ratio of sides work with the basic triangle above a 2 b 2 = c 2 1 2 ( 3) 2 = 1 3 = 4 = c 2 4 = 2 = c Using property 3, we know that all triangles are similar and their sides will be in the same ratio When to use TrianglesFind the altitude If you draw a vertex straight down it creates a triangle See picture below The triangle is a triangle I can use the rules to

30 60 90 Triangle Theorem Ratio Formula Video

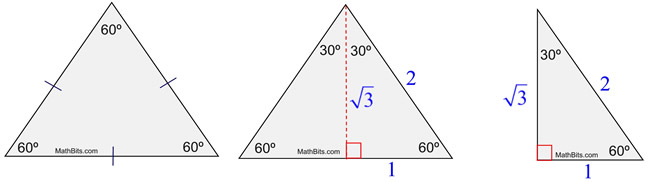
Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math

A triangle where the angles are 30°, 60°, and 90° Try this In the figure below, drag the orange dots on each vertex to reshape the triangle Note how the angles remain the same, and it maintains the same proportions between its sides This is one of the 'standard' right triangles you should be able recognize on sight30 60 90 Triangles E1 Find the hypotenuse of a triangle with a short side of 3 units Hypotenuse= Step 1 Use the formula 2*s Step 2 2*3 =6 units E2 Find the long side of a thirty sixty ninty triangle with a short side of 3 units Long leg = Step 1AAS Triangle Congruence Theorem Similar Polygons Similar Polygons and Proportions AA Triangle Similarity Postulate SAS Triangle Similarity Theorem SSS Triangle Similarity Theorem Altitude of a Triangle Median of a Triangle Concurrency of Medians of a Triangle 30°60°90° Triangle Theorem 45°45°90° Triangle Theorem Trigonometric Ratios

30 60 90 And 45 45 90 Triangle Calculator

1

A 30, 60, 90 triangle is one half of an equilateral triangle The three sides will be multiples of 1 for the short side, 2 for the hypotenuse, and the square root of 3 for the other side such that 2² = (√3)² 1² That is 4 = 3 1The graphics posted above show the 3 cases of a 30 60 90 triangle If you know just 1 side of the triangle, the other 2 sides can be easily calculated For example, if you only know the short side (figure5), the medium side is found by multiplying this by the square root of 3 (about 1732) and the hypotenuse is calculated by multiplying the short side by 2The triangle is a special right triangle, as it has a special relationship between its sides If we know the measure of at least one side of the triangle, the special proportions of sides of the triangle could be used to determine the measure of other sides of the same triangle

Trigonometry For Dummies Cheat Sheet Dummies

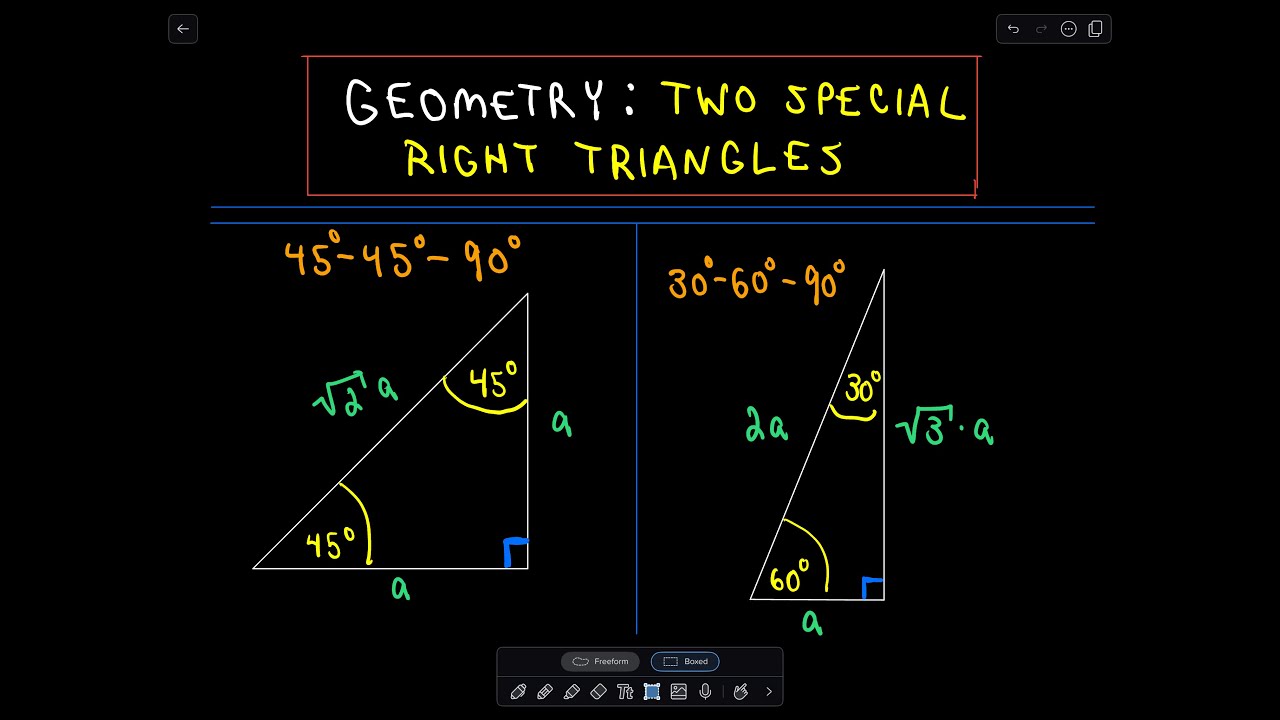
Special Right Triangles In Geometry 45 45 90 And 30 60 90 Youtube

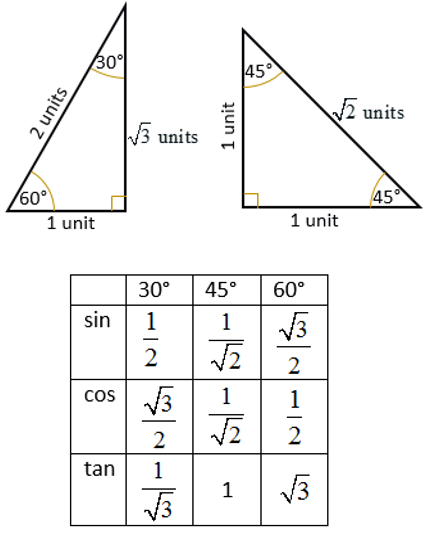
Formula chartpdf STAAR STAAR GEOMETRY REFERENCE MATERIALS TM State of Texas Assessments of Academic Readiness CIRCUMFERENCE Circle C = 2π r or C = Standard form of a linear equation Ax By=C STAAR GEOMETRY REFERENCE MATERIALS 30 ° 2 x x 60 ° x 3 30° – 60° – 90° triangle x x 45FORMULA CHART 2 of 2 45 – 45 – 90 Special right triangles 30 – 60 – 90 The sum of any two sides of a triangle must be greater than the third Sum of interior angles of a polygon Sum = (n2) 180 Sin A = opposite Cos A = adjacent Tan A = opposite1 divided by 2 To find, say, the sine of an angle measuring fortyfive degrees, you would trace across in the "sin" row and down the "45°" column, taking the squareroot symbol with you as you go and remembering to include the "divided by 2" from the bottom, to get sin(45°) = sqrt(2)/2

30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com

Right Triangles And Trigonometry Graphic Organizer Reference Sheets Freebie Trigonometry Right Triangle Math Methods

 A right triangle is a special right triangle in which one angle measures 30 degrees and the other 60 degrees The key characteristic of a right triangle is that its angles have measures of 30 degrees (π/6 rads), 60 degrees (π/3 rads) and 90 degrees (π/2 rads) The sides of a right triangle lie in the ratio 1√32For any problem involving a 30°60°90° triangle, the student should not use a table The student should sketch the triangle and place the ratio numbers Since the cosine is the ratio of the adjacent side to the hypotenuse, you can see that cos 60° = ½ Example 2 Evaluate sin 30° Answer sin 30° = ½ You can see that directly in the figure aboveThe following special angles chart show how to derive the trig ratios of 30°, 45° and 60° from the and special triangles Scroll down the page if you need more examples and explanations on how to derive and use the trig ratios of special angles Trigonometric Function Values Of Special Angles How to derive the

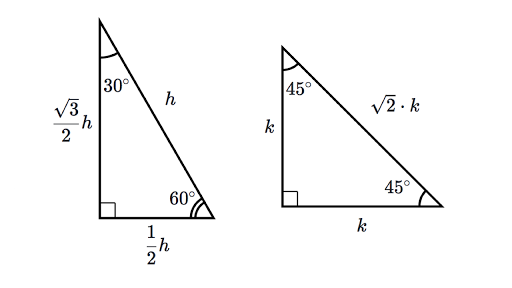
Special Right Triangles Review Article Khan Academy

Special Right Triangles 30 60 90 And 45 45 90 Triangles Matter Of Math

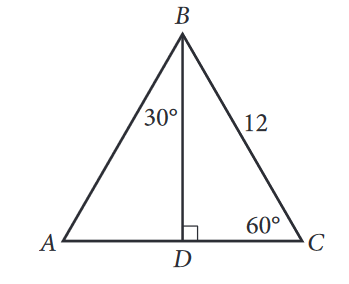
A triangle is a special right triangle that contains internal angles of 30, 60, and 90 degrees Once we identify a triangle to be a 30 60 90 triangle, the values of all angles and sides can be quickly identified Imagine cutting an equilateral triangle vertically, right down the middle Each half has now become a 30 60 90 triangle They want you to recognize that you're dealing with a triangle The ratios of the side lengths for a triangle can be found on your formula chart When you consult it, you see that across from the 30 degree angle is the smallest side (in this case, 1); A theorem in Geometry is well known The theorem states that, in a right triangle, the side opposite to 30 degree angle is half of the hypotenuse I have a proof that uses construction of equilateral triangle Is the simpler alternative proof possible using school level Geometry I want to give illustration in class room

Right Triangle Relationships

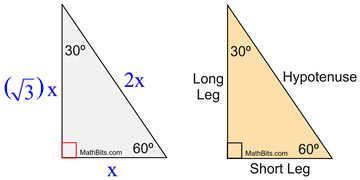
Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math

ChartToppers 100 The side opposite the 90* angle of a triangle If given the long leg in this triangle, this is how you find the length of the hypotenuse Divide 8 by √3, then multiply that answer by 2 In a triangle, you would use this formula when trying toThe lengths of the sides of a 30°60°90° triangle are in the ratio of 1 √3 2 You can also recognize a 30°60°90° triangle by the angles As long as you know that one of the angles in the rightangle triangle is either 30° or 60° then it must be a 30°60°90° special right triangle30°60°90° Triangles There is a special relationship among the measures of the sides of a 30 ° − 60 ° − 90 ° triangle A 30 ° − 60 ° − 90 ° triangle is commonly encountered right triangle whose sides are in the proportion 1 3 2 The measures of the sides are x, x 3, and 2 x

Gre Geometry Formulas Magoosh Blog Gre Test

30 60 90 Right Triangles Solutions Examples Videos

A right triangle (literally pronounced "thirty sixty ninety") is a special type of right triangle where the three angles measure 30 degrees, 60 degrees, and 90 degrees The triangle is significant because the sides exist in an easytoremember ratio 1sqrt (3)2 That is to say, the hypotenuse is twice as long as the shorter leg, and the longer leg is the square root of 3 times30 60 Triangle Calculator Area Perimeter Note Fill in any item and get the result of other items by clicking "Calculate" button 30 ̊ 60 ̊ Rad π/6 π/3 Sine 05 Cosine 05 Tangent Cotangent Formulas of triangle with angle 30̊, 60̊ and 90̊ • area = 05 * long side * short side;Please give me feedback on the comment Thanks a lot!!

Special Right Triangles 45 45 30 60 90 Notes Sheet Graphic Organizers

Special Right Triangles Fully Explained W 19 Examples

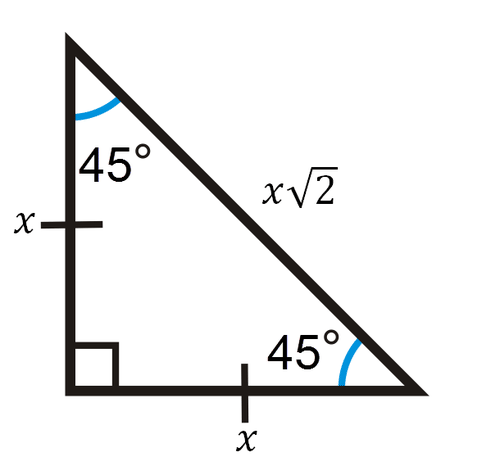
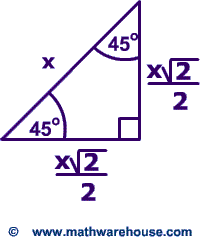
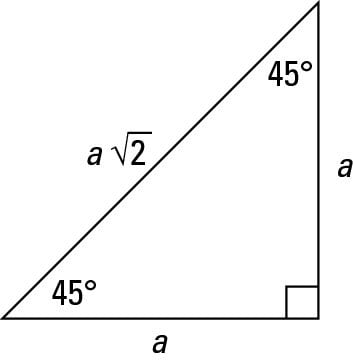
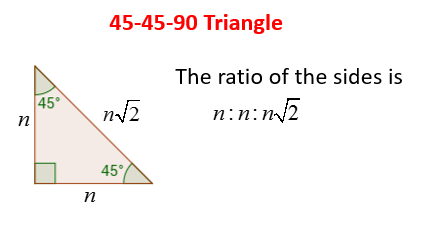
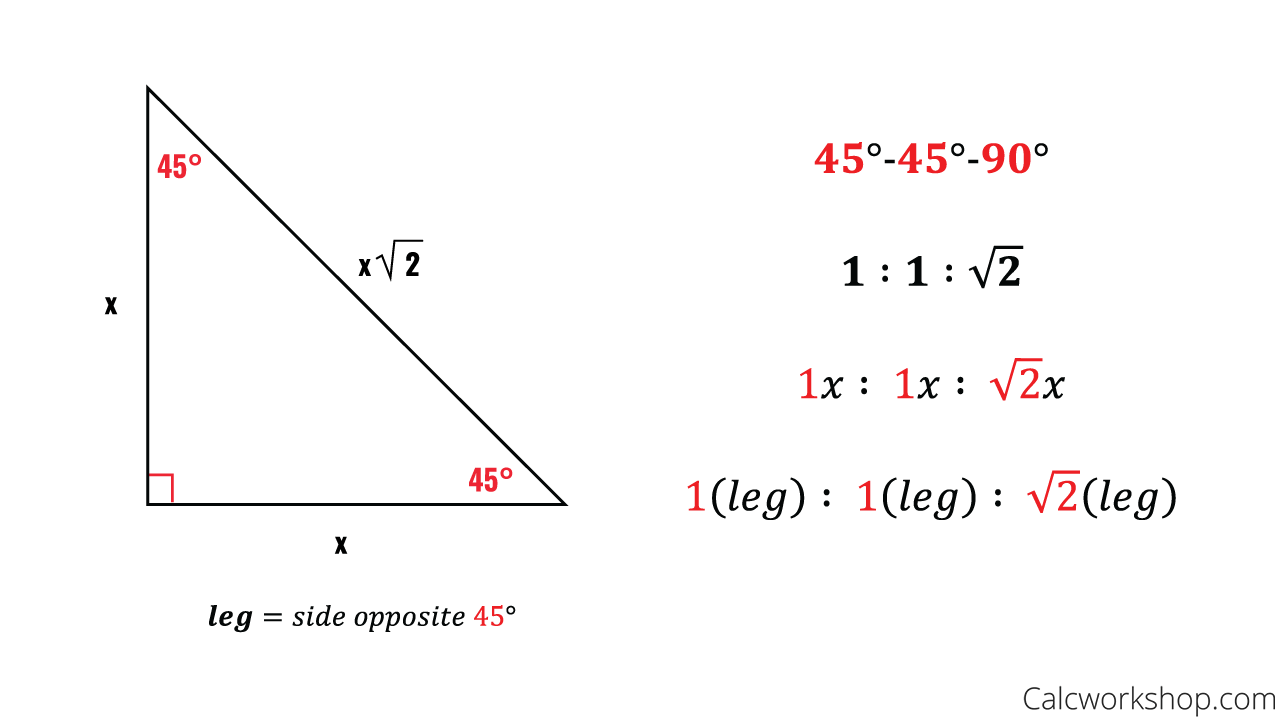
Consider a 30,60,90 triangle We know from converting radians and degrees, that these triangles are equivalent Here is it in radian form This second triangle is how the values are formed on the unit circle Now consider a 45,45,90 triangleMrs Lin These are the two most common right triangles For degrees, the ratio is 1 1 √ 2 For degrees, the ratio is 1 √ 3 2 Other concepts to remember are that in any triangle a larger angle corresponds to longer side and bsame angles have the same side length

Geometry Formula Sheet Pdf

Unit Circle Wyzant Lessons

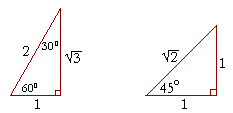
The 30 60 90 Triangle Topics In Trigonometry

1

30 60 90 Triangle Theorem Ratio Formula Video

30 60 90 Triangle Example Problem Video Khan Academy

Special Right Triangles Formulas 30 60 90 And 45 45 90 Special Right Triangles Examples Pictures And Practice Problems

Solve A 30 60 90 Triangle With Gradea

30 60 90 Triangle Rules Sides Ratio Of A 30 60 90 Triangle Video Lesson Transcript Study Com

How To Work With 30 60 90 And 45 45 90 Degree Triangles Dummies

30 60 90 And 45 45 90 Triangle Calculator

Special Right Triangles Activity Builder By Desmos

Trigonometric Ratios Of Special Angles 0 30 45 60 90 Video Lessons Examples And Solutions

30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com

30 60 90 Triangle Formulas Rules And Sides Science Trends

30 60 90 Formulas 30 60 90 Triangle Rule And Examples

45 45 90 Right Triangles Solutions Examples Videos

The Easy Guide To The 30 60 90 Triangle

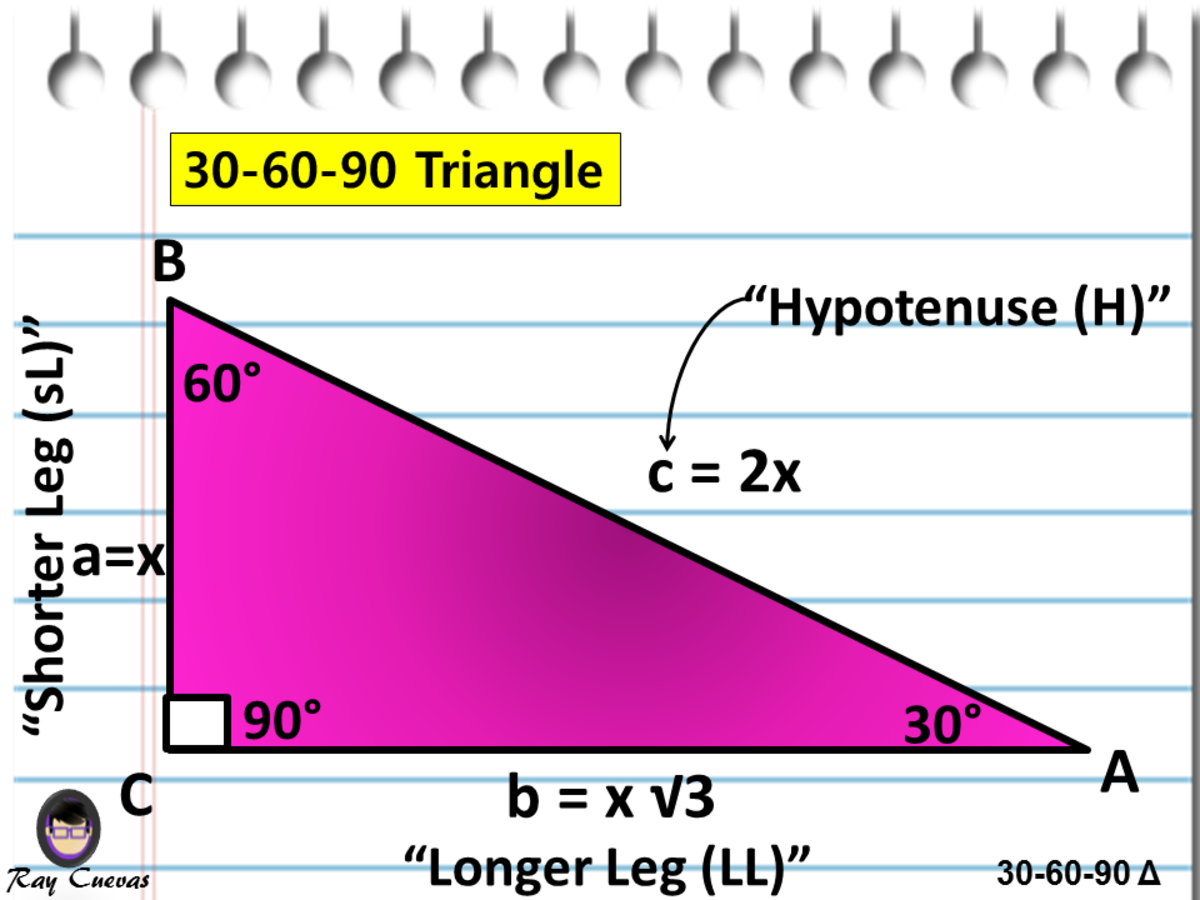
A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation

Unit Circle Wyzant Lessons

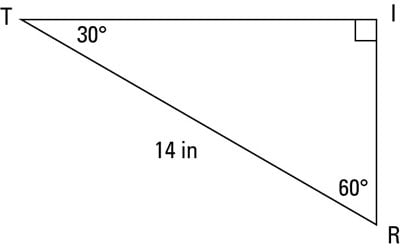
A Quick Guide To The 30 60 90 Degree Triangle Dummies

2

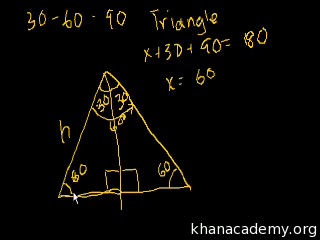
Special Right Triangles Intro Part 2 Video Khan Academy

Special Right Triangles 30 60 90 And 45 45 90 Triangles Matter Of Math

The Easy Guide To The 30 60 90 Triangle

1

45 45 90 And 30 60 90 Triangles Zona Land Education

30 60 90 Special Right Triangles Youtube

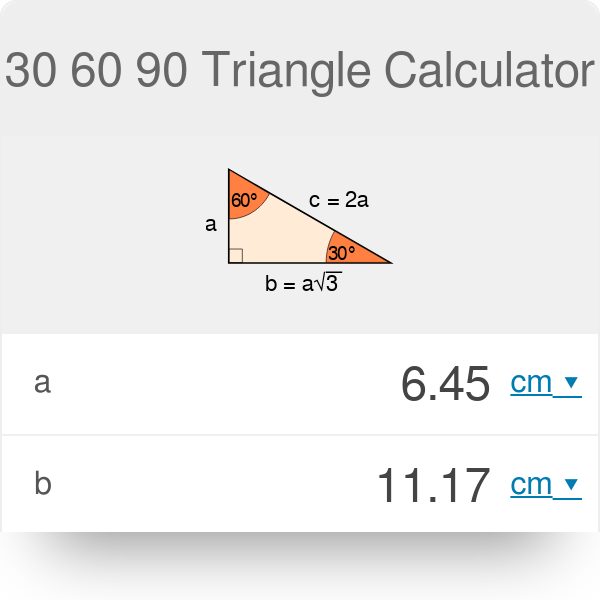
30 60 90 Triangle Calculator Formula Rules

Special Right Triangle Wikipedia

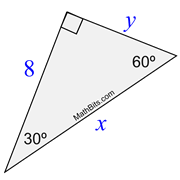
Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math

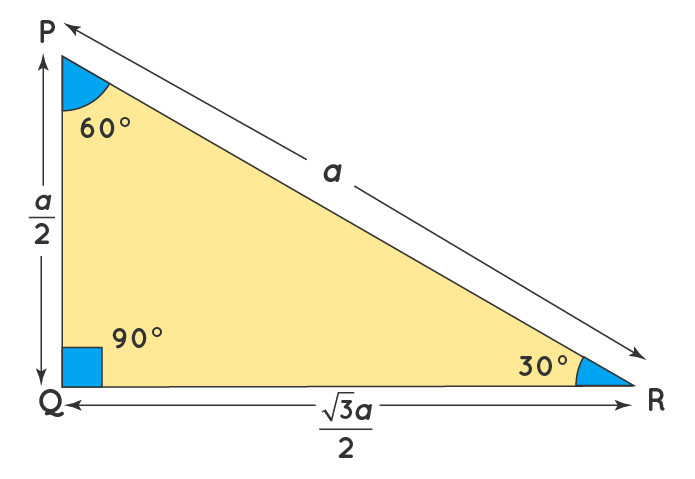
30 60 90 Triangle Definition Theorem Formula Examples

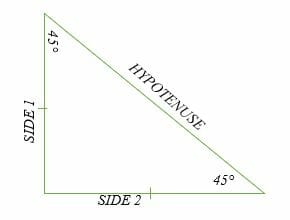
45 45 90 Triangle Explanation Examples

The Easy Guide To The 30 60 90 Triangle

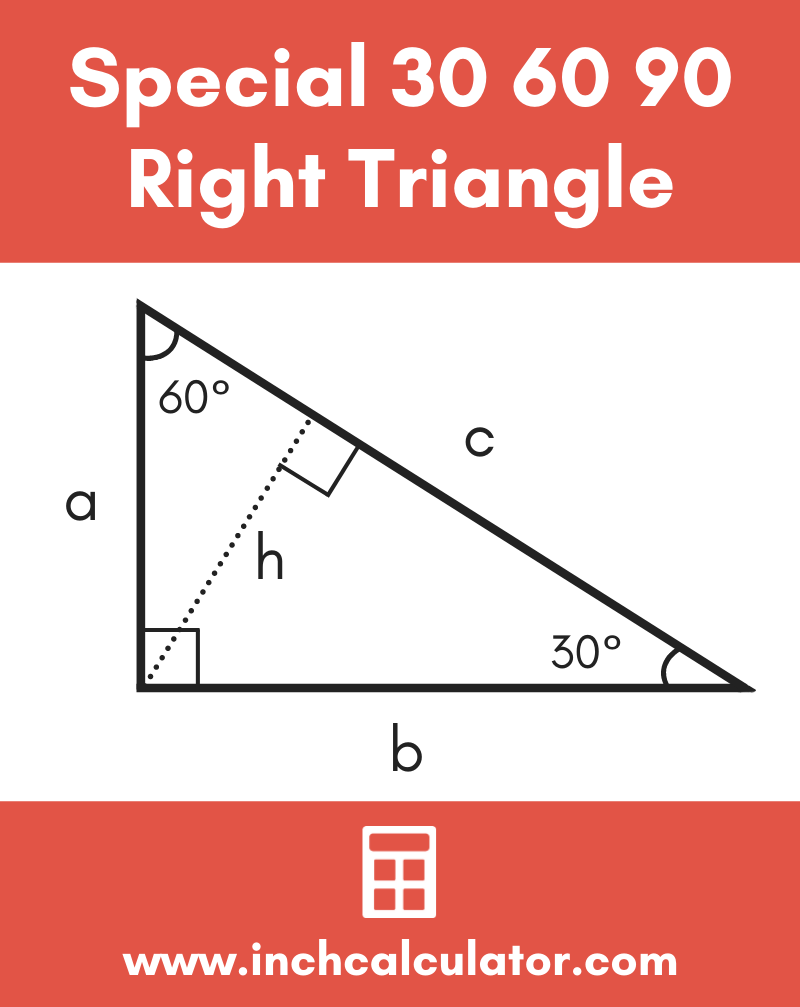
30 60 90 Special Right Triangle Calculator Inch Calculator

30 60 90 Triangle Calculator Formula Rules

30 60 90 And 45 45 90 Triangle Calculator

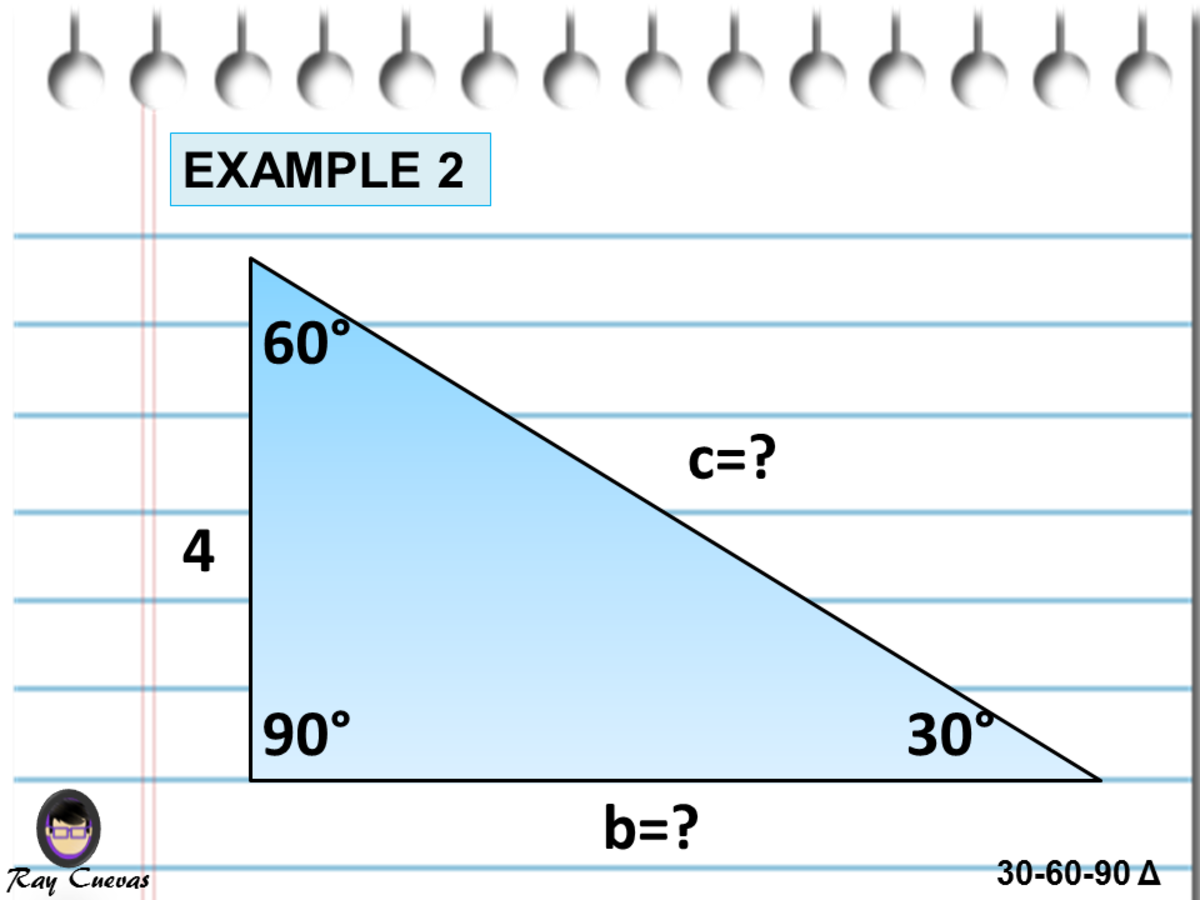
A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation

30 60 90 Right Triangles Free Math Help

45 45 90 Triangle Calculator Formula Rules

30 60 90 Triangle Theorem Ratio Formula Video

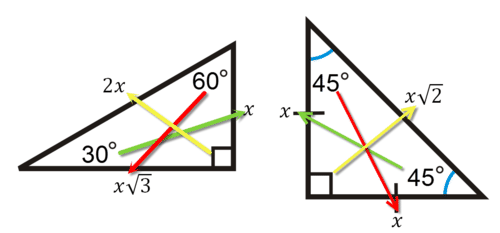
Special Right Triangles Ck 12 Foundation

30 60 90 Triangle Theorem Ratio Formula Video

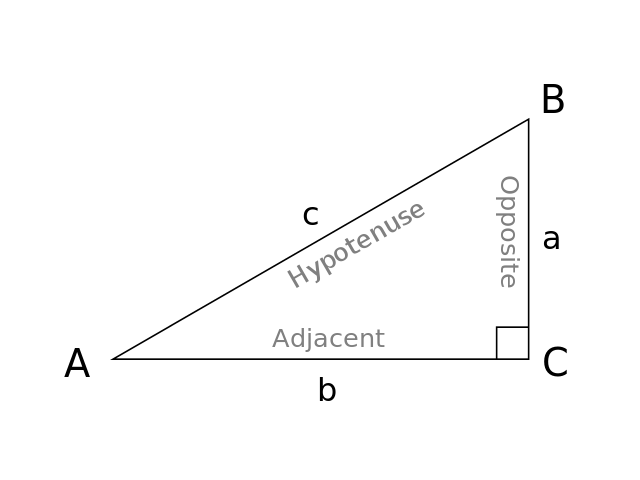
30 60 90 Triangle Formulas Rules And Sides Science Trends

Unit 7 Triangles And Area Ppt Download

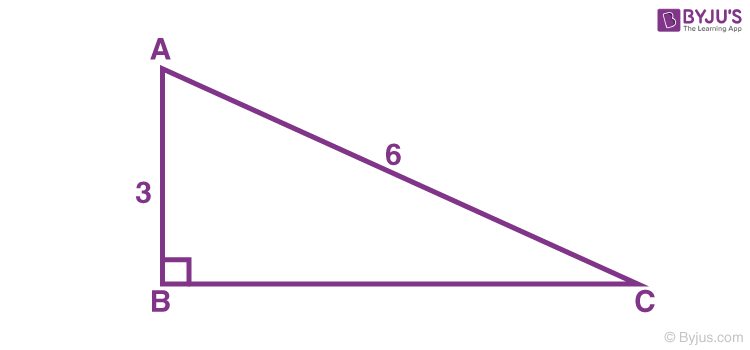
30 60 90 Formulas 30 60 90 Triangle Rule And Examples

1

A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation

Special Right Triangles 30 60 90 And 45 45 90 Triangles Youtube

30 60 90 Triangle Theorem Ratio Formula Video

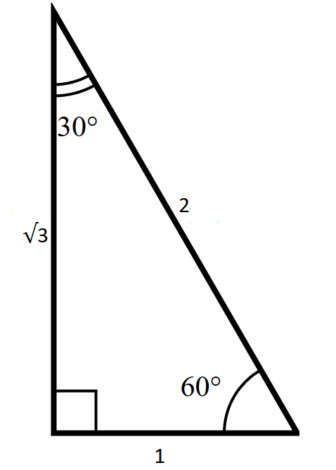
The Complete Guide To The 30 60 90 Triangle Collegevine Blog

Right Triangles Special Right Tris Notes Practice Task Cards Riddle Bundle Special Right Triangle Math Notes Gre Math

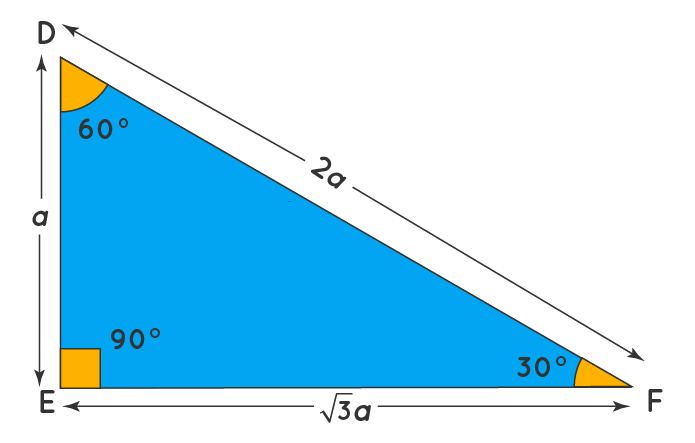
30 60 90 Triangle Definition Theorem Formula Examples

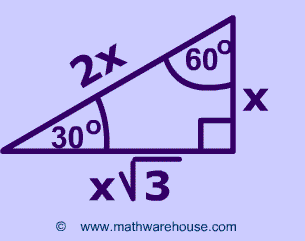
Special Right Triangles Formulas 30 60 90 And 45 45 90 Special Right Triangles Examples Pictures And Practice Problems

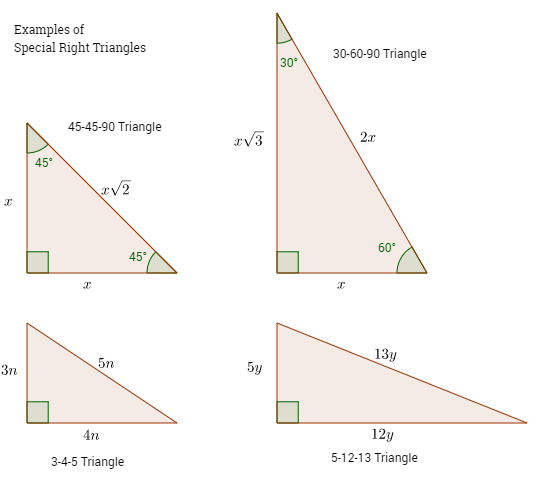
Special Right Triangles Video Lessons Examples And Solutions

30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com

190 High School Geometry Ideas Geometry High School Teaching Geometry Math Geometry

How To Find The Base Of A Triangle In 4 Different Ways

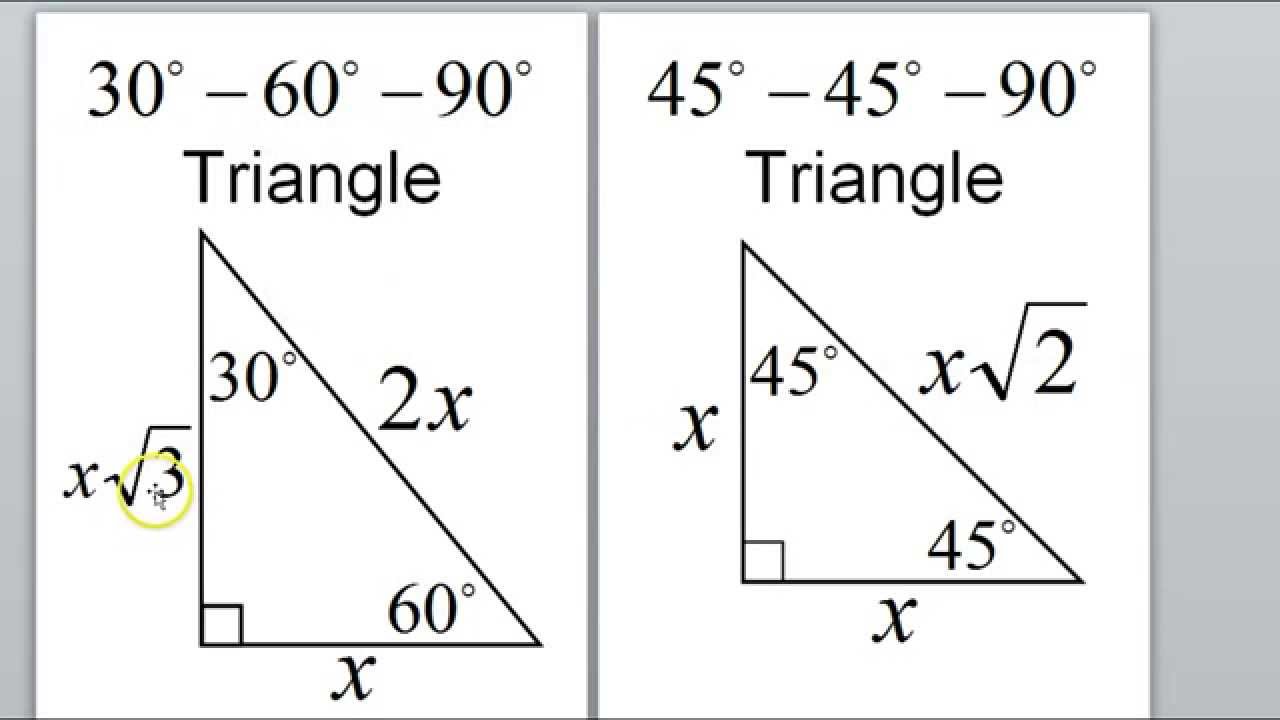
Day 1 Hw Special Right Triangles 45 45 90 30 60 90 Youtube

Trigonometry

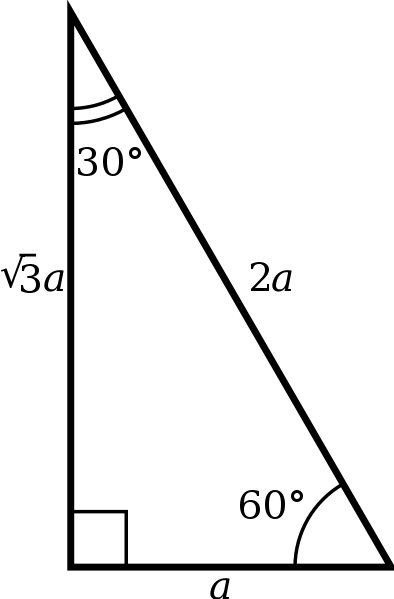
30 60 90 Triangle Formulas Rules And Sides Science Trends

Special Right Triangles Interactive Notebook Page Math Methods Teaching Geometry Math Interactive Notebook

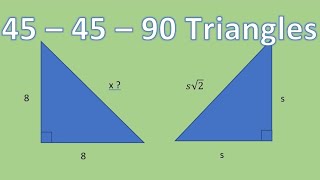
45 45 90 Right Triangles Solutions Examples Videos

Triand Easy Online Student Testing

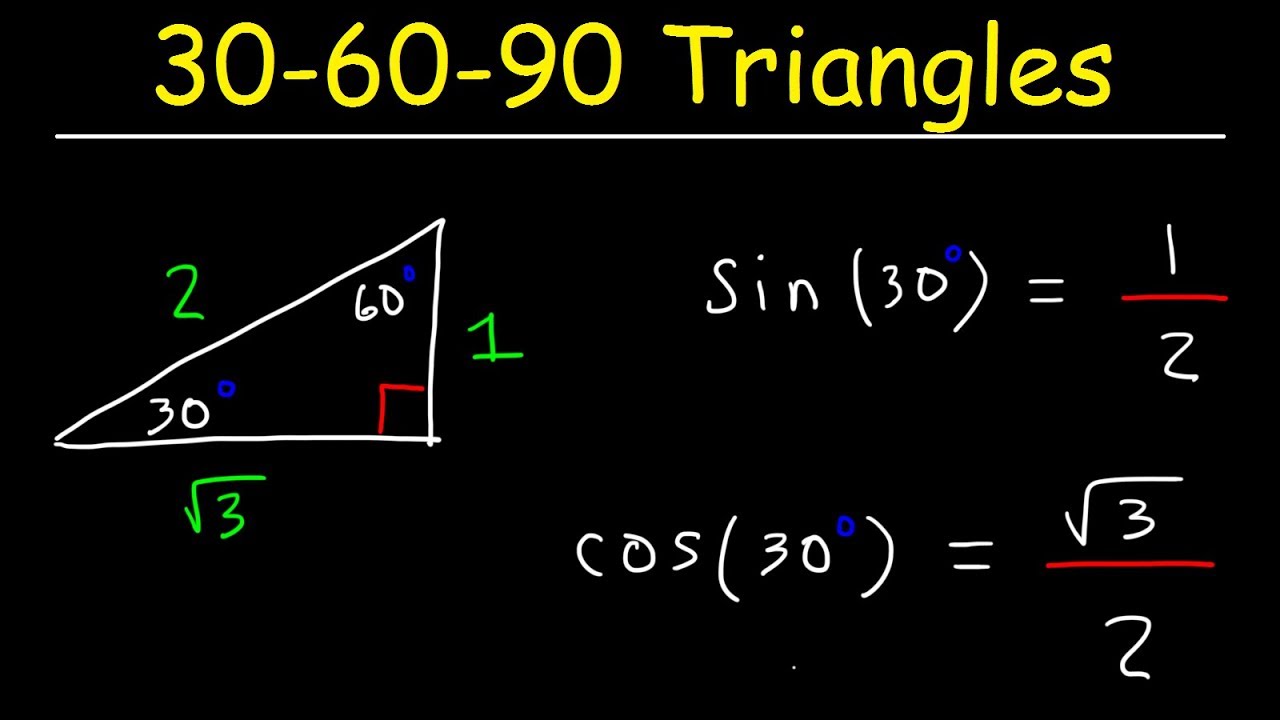
30 60 90 Triangles Special Right Triangle Trigonometry Youtube

Properties Of Triangle Types Formulas Video Practice

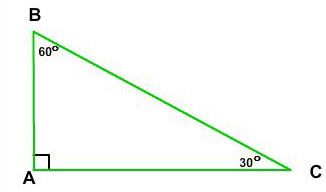
30 60 90 Right Triangle Side Ratios Expii

30 60 90 And 45 45 90 Triangle Calculator

30 60 90 Triangle Calculator Formula Rules

The Easy Guide To The 30 60 90 Triangle

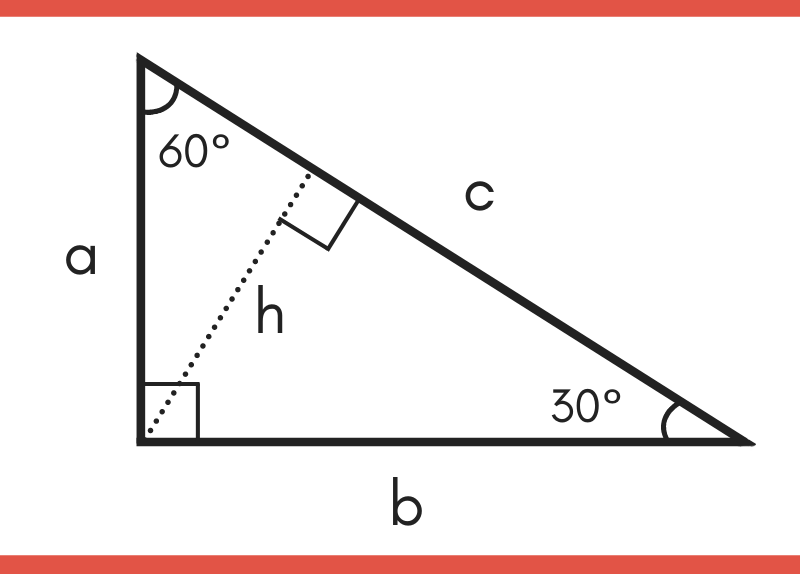
30 60 90 Special Right Triangle Calculator Inch Calculator

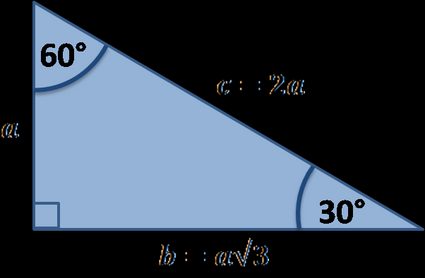
30 60 90 Triangle Calculator Formula Rules

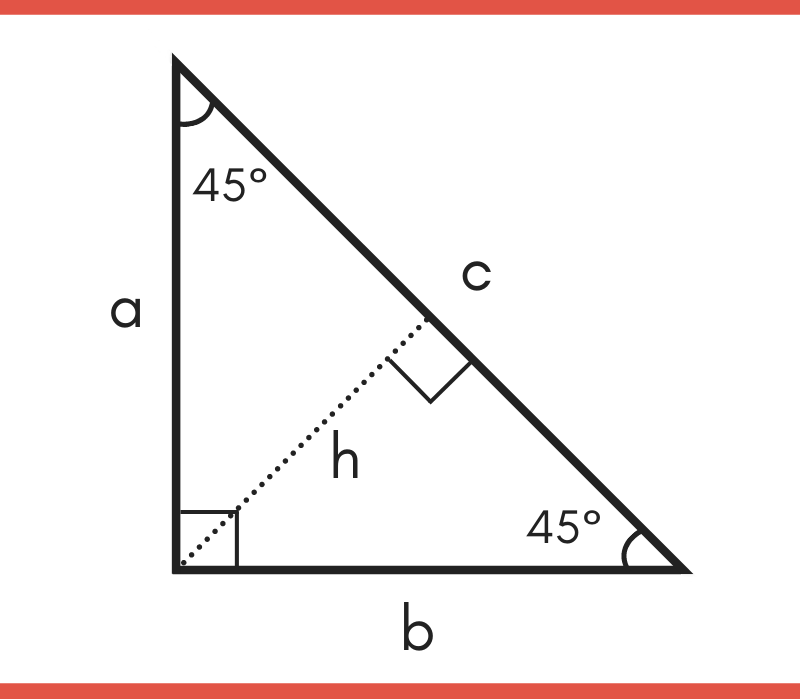
45 45 90 Special Right Triangle Calculator Inch Calculator

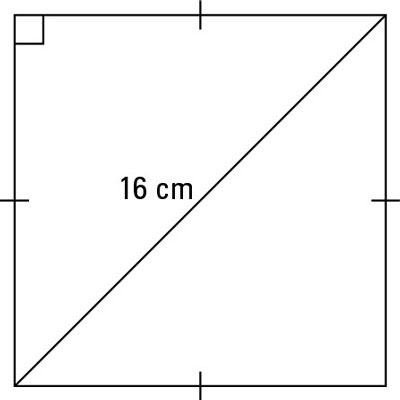
How To Work With 30 60 90 And 45 45 90 Degree Triangles Dummies

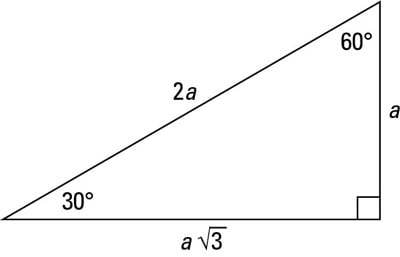
A Quick Guide To The 30 60 90 Degree Triangle Dummies

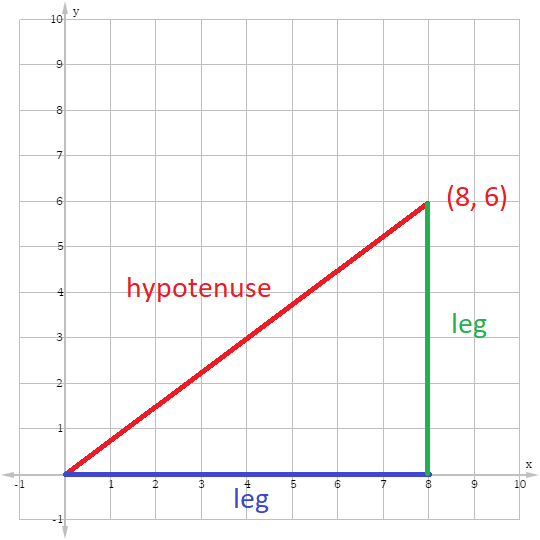
30 60 90 Triangle Formulas Rules And Sides Science Trends

30 60 90 Triangle Calculator Formula Rules

Special Right Triangles Fully Explained W 19 Examples

What Are The Side Relationships Of A 15 75 90 Triangle Quora

Special Right Triangles 30 60 90 And 45 45 90 Triangles Matter Of Math

30 60 90 Triangle Explanation Examples

30 60 90 Triangle Definition Theorem Formula Examples

Incoming Term: 30 60 90 triangle formula chart,